Is 120 VAC Really 120 Volts?
Let's take a look at the sine wave you would see if you hooked up an oscilloscope to a typical household power supply. This is showing reading line with respect to neutral.
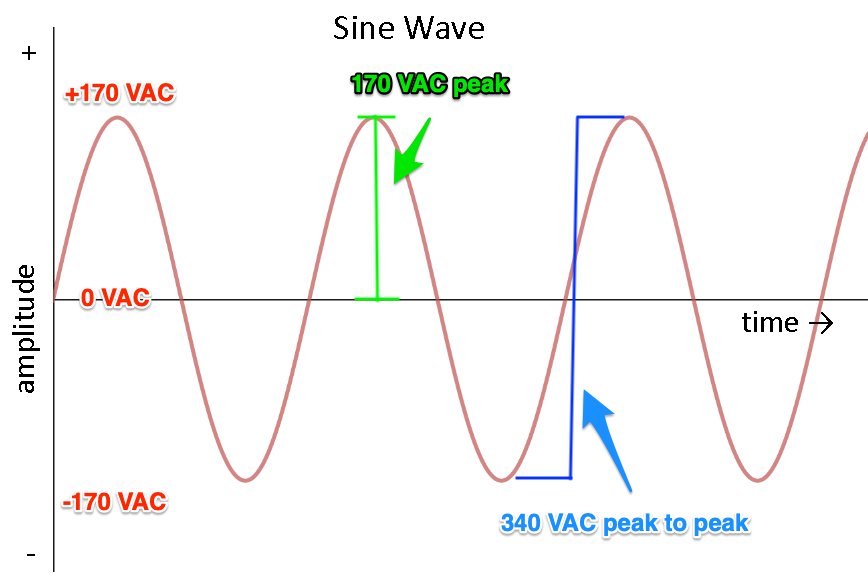
Hopefully you're already familiar with using a sine wave to represent AC voltage like this. To define a little terminology: the peak voltage (shown in green) is the voltage difference between the middle line (0 VAC) and the highest point of each peak. This diagram shows 170 VAC peak. Peak to peak voltage, on the other hand, is when you're talking about the difference between the positive peak and the negative peak. That's just 170 + 170 = 340 VAC peak to peak.
Now, I'm sure you've already noticed something odd: why am I showing a sine wave with 170 peak voltage? Is this some funky, special power supply that we're measuring?
Nope. As I said before, this is what you would see if you used an oscilloscope to measure one of the lines of a standard North American household power supply with respect to neutral. So why the 170 VAC peaks? Have we been wrong all this time talking about 120 VAC? Are our meters lying to us?
Of course not. What we're seeing here is the difference between AC peak voltage and RMS voltage. RMS stands for Root Mean Square (that's a math term which isn't important to dive into right now). Whereas peak voltage shows how much AC voltage we have at the highest points of the sine wave, RMS voltage shows us how much of that voltage we have that will do work over time.
To calculate RMS voltage from peak voltage, you simply have to divide the peak voltage by the square root of 2. If you remember from your math classes, the square root of 2 is irrational, but can be approximated as 1.41.
So if we want to find the RMS voltage of 170 VAC peak, we just do like so: 170 / 1.41 = 120 VAC. We've found our 120 volts!
Why do we bother to do this? If it takes an extra step to calculate the RMS voltage from the peak voltage, why don't we just talk about peak voltage all the time and save ourselves the worry?
It's because RMS voltage is the value that's actually practical. To demonstrate why, let's say you have a simple circuit consisting only of a resistor hooked up to a 100 VDC power supply. That resistor will produce some amount of heat due to the electrons pushed through it by that voltage. Now take that same resistor, but hook it up to a 100 VAC peak power supply. With this configuration, the resistor will produce less heat than with the 100 VDC configuration.
You can see why intuitively: in DC, that full 100 volts is present all the time, because there's no sine wave, no reversing polarity. So those 100 VDC will drive the same amount of current through that load constantly. But with 100 VAC peak, sometimes you have 100 volts, but other times you have 0 volts, or anywhere in between. The amount of current flowing through that resistor will fluctuate, and this means that, over time, less heat gets produced by 100 VAC peak when compared to 100 VDC.
When we calculate RMS voltage, we're figuring out the amount of DC voltage that will produce the same power output in a load as a particular amount of AC peak voltage will. Divide 100 VAC peak by 1.41, and you get ~70 VAC RMS. That means that 100 VAC peak will result in the same amount of power output from a load as 70 VDC will.
If you want to calculate the power output of a load, you use the Ohm's law equation P = E^2 / R. That E stands for volts, and the volts you plug into that equation must be RMS volts (if you're dealing with AC). Otherwise, your answer won't be meaningful.
So here's your takeaway: when we as techs talk about VAC, what we're always actually talking about is RMS voltage, because that's the voltage that's practical to talk about. If you want to talk about peak voltage, you have to specify that that's what you're talking about. And if you see a sine wave alternating between 170 volt peaks on your oscilloscope when measuring household power, now you know why.
Want to continue deepening your knowledge so you can be the best tech you can be? Click here to check out our courses at the Master Samurai Tech Academy.
-
.png) 5
5






4 Comments
Recommended Comments